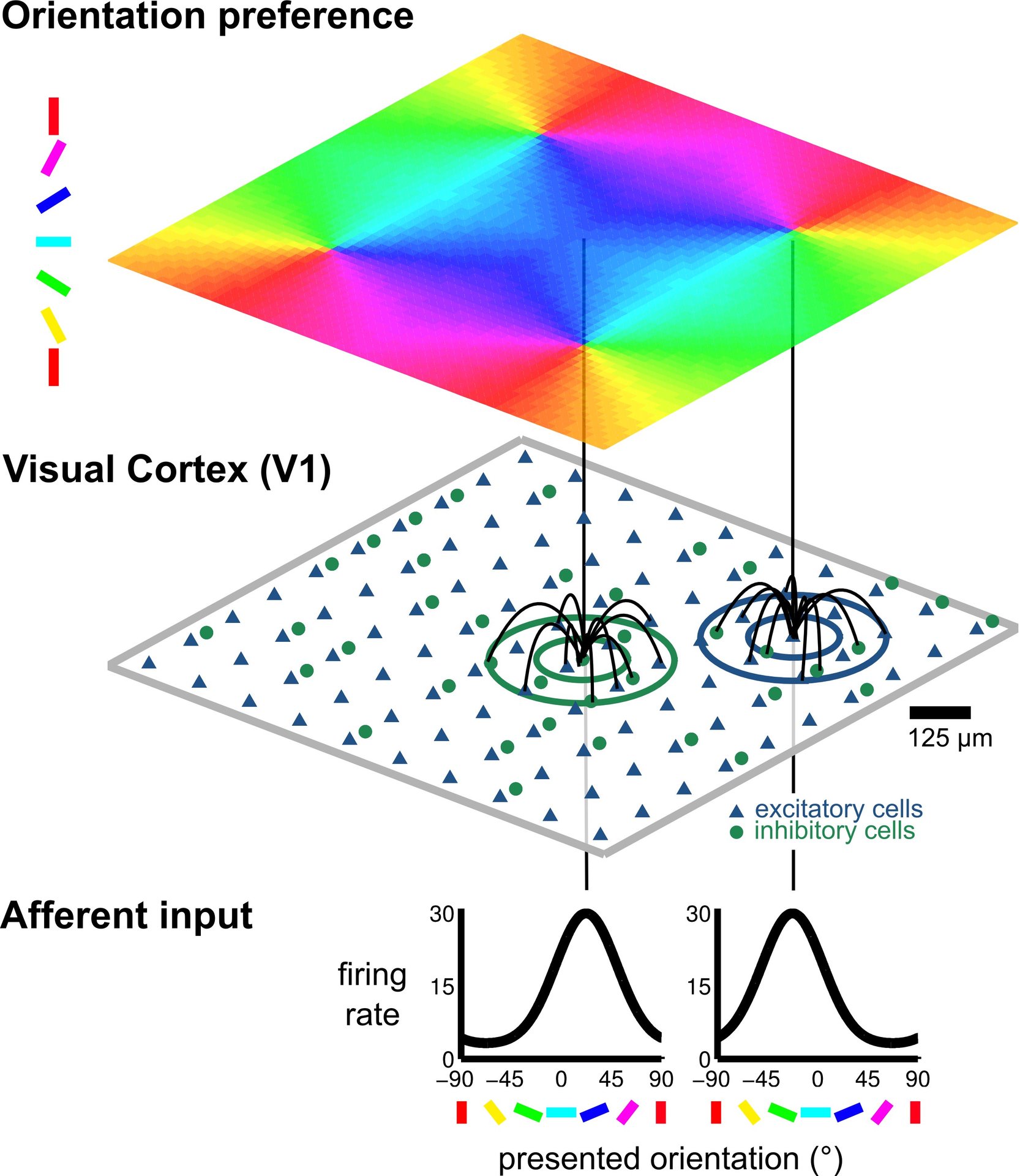
 © NI, TUB
© NI, TUB
Aktuelles
Keine Nachrichten verfügbar.
Kommende Veranstaltungen
Keine aktuellen Veranstaltungen gefunden.
Standort
Gebäude
 © NI, TUB
© NI, TUB
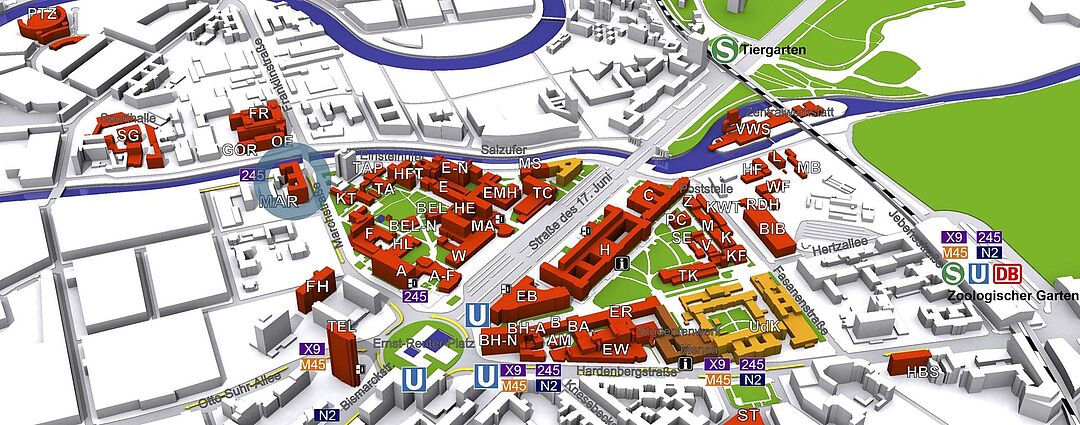 © TU Berlin, Abt. IV Gebäude-/Dienstemanagement
© TU Berlin, Abt. IV Gebäude-/Dienstemanagement
Die Arbeitsgruppe "Neuronale Informationsverarbeitung" befindet sich im Haus in der Marchstrasse 23 (MAR) im 5. Stock.
Kontakt
Neuronale Informationsverarbeitung
| Einrichtung | Technische Universität Berlin |
|---|---|
| Sekretariat | MAR 5-6 |
| Gebäude | MAR |
| Adresse | Marchstrasse 23 10587 Berlin |
Leiter
| Gebäude | MAR |
|---|---|
| Raum | MAR 5043 |
| Sprechstunden Fr | 12:00-13:00 |
Sekretariat
| Sekretariat | MAR 5-6 |
|---|---|
| Gebäude | MAR |
| Raum | MAR 5042 |
| Sprechstunden Mi | 9:00-11:00 |

 © NI, TUB
© NI, TUB
 © NI, TUB
© NI, TUB